The Lydian Mode

Home » Piano Theory » The Lydian Mode

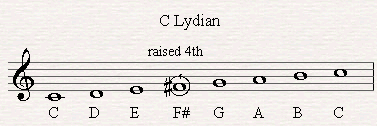
The mode is created by playing the notes of a major scale starting from the fourth note. Here's an example of the mode starting from F, based on a C major scale.

Here's the formula of the Mode:

Whole Step - Whole Step - Whole Step - Half Step - Whole Step - Whole Step - Half Step

How to use the Lydian mode?

The mode could help us solving the tension created by the clash between the fourth note and the third note of the scale.

Let's play C major scale over a C chord for example.

If we'll play the scale starting from C we're on the safe side since F is a passing note and therefore does not clash with the third note of C major (E).

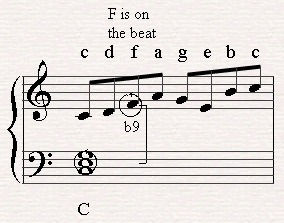
However if we play a melodic line which involves the F on one of the beats of the bar the F note will sound dissonant since the it will create of a b9 with the E note of the chord.

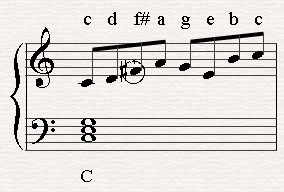
The way to avoid this and in the same time to give our line a jazzy feel is to replace F with F# making it the raised 4th of the scale.

The result would be creating the mode (Starting from C). The Mode derives from G major starting from the 4th note.

If you desire to play the mode over a seventh chord (C7 chord for example) you can simply lower the seventh note of the mode and create the Lydian dominant scale.

Here's An example of how the mode is being used when improvising:

Many jazz players and singers like to end up their pieces on the raised 4th.
In the next case I show how Sarah Vaughn ends on F# in the song "Lover Man Where Can You Be".
She does it so brightly. suggesting the mode instead of a major scale on the last chord.

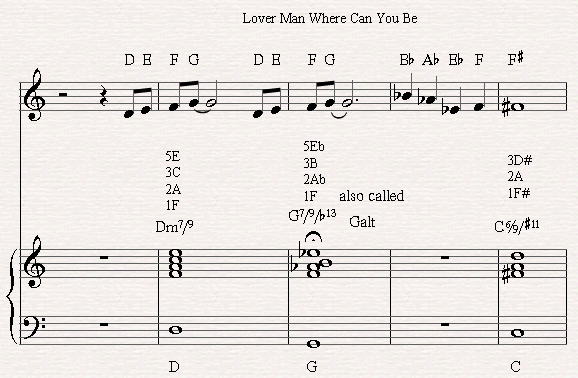
If you'd like to know more about the chord played in this example I suggest you click here to go to the Raised 11th chords.

Compositions in the Mode

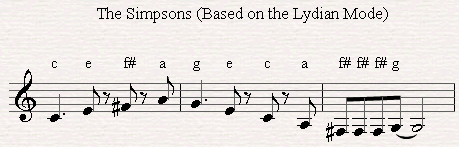
The theme for "The Simpsons" is sometimes cited as being in the Lydian mode, and this is certainly true for the first few bars.

However, later passages in the theme include a minor 7th, along with other notes characteristic of the Lydian mode, and that thus places those passages in the Lydian Dominant Scale, which is sometimes thought wrongly to be another mode, or related to the modal system.

The Kill by 30 Seconds to Marts Eden by Hooverphonic

The "To Kill a Mockinbird" score by Elmer Bernstein features the mode.

"Man on the Moon" by R.E.M (The verse)

"Dancing Days" by Led Zeppelin (The intro)

"Unravel" by Bjork"

"Little Red Corvette" by Prince

"Love Like This" by Faith Evans

"All I Need" by Radio Head

Music Modes

The Ionian Mode
The Dorian Mode
The Phrygian Mode
The Mixolydian Mode
The Aeolian Mode
The Locrian Mode

Return from the Lydian mode to Piano Theory.

How To Play Piano by Chords

THE FAST AND EASY WAY TO LEARN PIANO!

The Ultimate Piano by Chords Learning Kit
Check It Out Now!

"Your entire site is simply fantastic. I really loved it. Now I am learning the basics of piano by myself, with your really great help. Thank you very much!"

Jaime C. from Brazil

"I only started to play about six weeks ago but the last hour of watching your videos about chord progressions has been something of a revelation. You're brilliant!!!!"

Stephen Roberts from U.S.A

"I'm a beginning keyboard player and your video's are an excellent guide. You're absolute not in a hurry, and take time to explain. I'm sure I'll follow all your lessons to get the hang of playing the piano/keyboard!"

Wouter E. from the Netherlands

"Thanks for all your work ( tuto and others ). You're doing a really great job, You're the best internet teacher I know."

Anthony Hassen Cohen from France